BISC110/S13: Series 1 Lab 3 Tetrahymena Investigation: Difference between revisions
| Line 80: | Line 80: | ||
#Double-clicking on either axis will allow you to change the scale, font and other features of the axis. | #Double-clicking on either axis will allow you to change the scale, font and other features of the axis. | ||
== PART II: Ink and ''Tetrahymena'' | == '''PART II: Ink and ''Tetrahymena'' Behav'''ior == | ||
You will be provided with 1% India ink and live ''Tetrahymena'' for this lab. You will add 1% ink to the ''Tetrahymena'' and make observations. Based on your careful observations, you will collect some data to quantify ''Tetrahymena'' phagocytosis in the presence of India ink. | You will be provided with 1% India ink and live ''Tetrahymena'' for this lab. You will add 1% ink to the ''Tetrahymena'' and make observations. Based on your careful observations, you will collect some data to quantify ''Tetrahymena'' phagocytosis in the presence of India ink. | ||
Revision as of 08:38, 3 January 2013
Objectives: In this lab you will learn:
- Scientific observation
- Measurement of specimens using the micrometer
- Experimental design
- Effective Figure design
Series 1 Lab 3 Tetrahymena pyriformis Phagocytosis
Adapted from Bozzone, M.D., and D.A. Martin 2000. An experimenal system to study phagocytosis. Pages 405-415, in Tested studies for laboratory teaching, Volume 21 (S.J. Karcher, Editor). Proceedings of the 21st Workshop/Conference of the Association for Biology Laboratory Education (ABLE).
In this laboratory, you will study Tetrahymena phagocytosis in the presence of India ink. You will have the opportunity to make scientific observations and learn some of the ways that scientific data are evaluated and presented.
NEED INTRO INFORMATION ON PHAGOCYTOSIS
PART I: Concepts in Experimentation
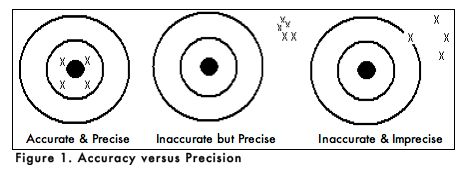
A. Accuracy and Precision
When carrying out an experiment, it is important to do the experiment more than one time to be sure that your measurements are accurate and as precise as possible. Accuracy is the degree of agreement between the measured value of a particular component and the accepted true value. Precision is defined as the degree of agreement between replicate measurements of the same component. Precise measurements do not necessarily indicate accurate measurements. Figure 1 uses targets to illustrate the difference between accuracy and precision. If the bull’s eyes in the targets below represent the true value, then the darts that are the closest to the center of the target are the most accurate. Darts that are not near the center of the target are not accurate even though they may be very closely grouped together indicating good precision. Finally, the darts that are not near the center or grouped together are neither accurate nor precise. Measured values that are both accurate and precise are the goal of all analytical procedures.
As with all analogies, the one above does not address an important issue that comes up in scientific experimentation. For example, when you observed the Tetrahymena after 15 minutes in the 1% ink solution, did each of the 10 cells that you counted have the same number of filled phagocytic vacuoles? If not, were you inaccurate or imprecise in your data collection? Or, is it possible that another factor accounted for the data you collected? Do you expect every individual Tetrahymena to behave the same in the presence of ink? Why or why not?
B. Statistical Parameters
For various reasons, replicate analytical measurements do not always result in exactly identical values, and so statistical calculations are often used to evaluate analytical data. The validity of these calculations is linked to the number of replicate measurements, so a high number of measured values will yield the most valid statistical evaluation. A short explanation of several elementary statistical parameters on replicate measurements are provided below.
1. Median Value
If all the replicate values for a series of measurements were ordered from the lowest value to the highest value, then the midpoint value is the median. For example, if a series of measured millimolar (mM) concentrations of NaCl are 10.1, 10.2, 10.3, 10.5, and 10.7mM, the median value would be 10.3mM.
2. Range of Values
The range is the difference between the highest measured value and the lowest measured value in a series of replicate measurements, and is a simple indicator of precision. A wide range in replicate measured values indicates poor precision. The range is calculated by subtracting the lowest replicate value from the highest. For the above concentrations of NaCl, the range would be calculated as:
3. Mean Value
The mean value is simply the arithmetic average of all the replicate values, and is generally considered to be more accurate than any individual measured value. The mean is calculated by adding all the measured values and dividing by the number of measured values or sample size. The mean value is represented mathematically as:
The mean of the NaCl concentrations from step #1 is calculated as follows:
4. Standard Deviation
The standard deviation is a measure of how spread out or variable the values are. The standard deviation is calculated by subtracting the mean from each value and then squaring and summing these values. The resulting value is divided by n-1, where n is the number of values. The square root of these values is the standard deviation. The standard deviation is represented mathematically as:
The standard deviation of the sodium chloride values is calculated as follows:
5. Practice Data Analysis
Imagine that you exposed Tetrahymena to ink and observed the number of ink filled vacuoles in 15 cells at both 10 minutes and 30 minutes. You obtained the following data for the number of filled vacuoles at each time point:
Calculate the means and standard deviations of ink filled vacuoles at 10 and 30 minutes. Refer to the Generating Graphs and Error Bars with Microsoft Excel instructions found below or in Appendix A and plot the data in a bar graph with time on the X axis and the mean number of filled vacuoles on the Y axis. Use error bars to denote the standard deviation.
Generating Graphs and Error Bars with Microsoft Excel
- To launch Excel, click on the icon in the dock at the bottom of the screen. An Excel Workbook will open. If Microsoft Excel is already open, select New Workbook from the File menu to display a new spreadsheet.
- To determine the mean and standard deviation, write Average in cell A2 and Standard Deviation in cell A3. List variable 1 in cell B1, variable 2 in cell B2… Now enter the number of filled vacuoles per cell for variable 1 in cells B4, B5, B6... Enter the number of filled vacuoles per cell for variable 2 in cells C4, C5, C6…

- Be sure that the formula builder bar under view is selected.
- To determine the average value for variable 1 (10 min), click on cell B2, press the = symbol, click on the upper left pull down menu and select AVERAGE, highlight cells B4-B18 and press return. The average value should now appear in cell B2.
- To determine the standard deviation for variable 1, click on cell B3, press the = symbol, click on the upper left pull down menu and select STDEV, highlight cells B4-B18 and press return. The standard deviation value should now appear in cell B3.
- To determine average and standard deviation values for variable 2 (30 min), highlight cells B2 and B3, select the lower right square on the highlighted box with the black + symbol, drag to the right until you reach cells C2 and C3, and then release the mouse. The average and standard deviation values for variable 2 should now appear in cells C2 and C3.
- To make your graph, click on cell A1. While keeping the mouse clicked, drag mouse to cell C3 so that cells A1, A2, B1, B2, C1, and C2 are all highlighted.
- Click on the Charts tab below the toolbar. A gallery of chart types will appear below. Press the Column button below to display the appropriate charts in this so-called Elements Gallery.
- To select the proper chart type from the Elements Gallery, press the “Clustered Column” thumbnail (all the way to the left). A chart will appear on the worksheet.
- Open the Formatting Palette by pressing on the Toolbox icon. Under Chart Options you can label the axes and provide a title.
- To add error bars, double click on the columns on your graph. The format data series box will appear. Select Error Bars on the left. Under display, select Both. Under error amount, select Custom and Specify Value. The Custom Error Bars chart will appear. Clear any values in the Positive Error Value box and then highlight the standard deviation values that you calculated previously. Do the same with the Negative Error Values. Click OK twice.
- The chart may be created as an object in the worksheet, or it may be displayed as a new sheet. Under the Chart menu select Move Chart... to choose between these two options.
- Double-clicking on either axis will allow you to change the scale, font and other features of the axis.
PART II: Ink and Tetrahymena Behavior
You will be provided with 1% India ink and live Tetrahymena for this lab. You will add 1% ink to the Tetrahymena and make observations. Based on your careful observations, you will collect some data to quantify Tetrahymena phagocytosis in the presence of India ink.
A. Observations of Tetrahymena pyriformis Exposed to India Ink
- In a microcentrifuge tube, add 50 μL of 1% ink solution and then add 50 μL of live Tetrahymena. Mix gently and record the time.
- What is the effective concentration of the ink after the addition of Tetrahymena?
- Add 20 μL of the Tetrahymena pyriformis and ink solution that you made in step 1 to a glass slide. Add a cover slip and view using the microscope. If you need to review how to focus the microscrope, refer to the directions in Lab 1. You may need to adjust the field diaphragm or to lower the condenser a bit to see the cellular structures clearly. Record your observations in your notebook.
- Do you see any ink particles inside the Tetrahymena? Be sure to note the time as soon as you notice an ink filled phagocytic vacuole forming. Continue observing the Tetrahymena. Watch the Tetrahymena for 15 minutes, noting how many vacuoles form and where those vacuoles are in the cell. Do they move? Are the vacuoles uniform in size?
B. Time course experiment of Tetrahymena pyriformis Exposed to India Ink
After you have had a chance to observe the "Tetrahymena" in the presence of ink, you will do an experiment in which you collect data to present in the form of two figures.
- Put on a pair of gloves.
- To begin your experiment, add 50 μL of 1% ink solution and then add 50 μL of live Tetrahymena. Mix gently and record the time.
- After 0, 5, 10 and 15 minutes, add 20 μL of the Tetrahymena and ink solution to a clean labeled microcentrifuge tube. IN THE HOOD, add 10 μL of 3% gluteraldehyde to your Tetrahymena and ink solution and wait for 1 minute. The gluteraldehyde will fix (kill) the cells, allowing you to observe the Tetrahymena in more detail. Then add 2 μL of 2.5 M glycine to inactivate the gluteraldehyde. Wait for 1 minute and then remove the tube from the hood.
- Add 20 μL of the resulting 32 μL mixture to a glass slide and place a cover slip on top.
- Using a digital camera, take photos of the Tetrahymena at the 0, 5, and 15 minute timepoints. Please refer to the directions in Appendix H for detailed camera instructions.
- Count the number of ink filled vacuoles in 10 individual Tetrahymena at each time point and record this information in your lab notebook.
- Using the micrometer, measure the size of these phagocytic vacuoles inside the Tetrahymena. Measure at least 1 vacuole from at least 5 individual Tetrahymena. Check with your instructor to be sure that you are measuring the correct structure. Did you see them form in step 1? Describe the process of phagocytosis in Tetrahymena in your lab notebook.