IGEM:IMPERIAL/2006/project/Oscillator/Theoretical Analyses/Results/2D Model1: Difference between revisions

From OpenWetWare
Jump to navigationJump to search
mNo edit summary
 
(46 intermediate revisions by 2 users not shown)
Line 1: Line 1:
== 2D Model 1 : Lotka volterra ==
<font size="6"><center>'''Model 1: Lotka-Volterra'''</center></font size="6">
*Lotka Volterra is the most famous and fundamental model to describe the interaction between the prey and predator
<br><br><br>
 
= '''Introduction''' =
= '''Introduction''' =
<b>Lotka-Volterra Equation</b>
<font size="4">'''Generalities''' </font size="4">
*Earliest known model proposed for a predator-prey system
<br><br>
*Natural oscillation of population of predator and prey
:*Lotka Volterra is the earliest (and most famous) population model.
*Modelled by a pair of first order, non-linear, differential equations, describing the dynamics of biological systems in which the predator and prey interact
:*It is built upon a pair of first order, non-linear, differential equations, describing the dynamics of ecological systems in which predators and preys interact
[[Image:LotkaV.png|center]]
<br>
<font size="4">'''Basic Assumptions of the Model''' </font size="4">
<br>
:* The growth of the prey population X is due to natural reproduction of the preys. In the case of Lotka-volterra the growth is proportional to the population
:* The population of preys is controlled by the hunting carried out by the predators (the natural death rate of the prey is assumed negligible compared to the killing rate due to the predators). In the present case the population decay is proportional to the population of both preys and predators.
:* The predator’s growth is the direct result of hunting the preys. In the present case it is proportional to the population of both preys and predators.
:* Finally the population of the predators is controlled by its natural death (proportional to the population)
<br><br>
<font size="4">'''Relevance of Lotka-Volterra to the 2D Model'''</font size="4">
<br><br>
:*The Lotka-Volterra model is probably the simplest prey-predator model  and is widely known to yield oscillating populations. It is therefore an ideal candidate as a starting point for our series of analysis.
:*However, it is straightforward to see that the assumptions it is based on are very different from the assumptions of our model. We therefore cannot expect to learn too much about our own system.
:*Furthermore, as we shall see, this model has a critical flaw regarding stability of its oscillations.
 
= '''Basic Results on the Steady Points and Vector Field''' =
 
<font size="4">'''Steady Points'''</font size="4">


<b> Basic Assumptions of the Model </b>
:*The Lotka-Volterra model has two steady points:
* The prey has unlimited exponential growth
::- The origin (0, 0)  
* The prey does not die itself, its death is only caused by predator
::- (d/c, a/b) (interestingly the steady population of the preys depends only on parameters associated to predators and vice-versa).
* The predator’s growth is upon its killing of prey, and it will have its natural decay
:* After Jacobian analysis, it can be shown that the stationary point (0, 0) is a saddle point, while (d/c, a/b) is a centre (that is the vector field will rotate around the point without being attracted or repelled by it).
<b>Relevance of the Model</b>
*Assume 2-D assumption is valid, i.e. the production and death of AHL and LuxR behave the same way
*The prey is AHL, and the predator is aiiA
**AHL will bind with the promoter in the prey cell, and hence more AHL will be produced, thus AHL is capable of reproducing itself
**AHL will be degraded by the enzyme aiiA, thus the degradation rate depends on the encounter rate with aiiA
**AHL is quite stable, the self-degradation rate is much smaller than the degradation rate caused bt aiiA, hence we assume aiiA does not degrade itself
**AHL will bind with LuxR and promote the production of aiiA and LuxR, hence the production rate of aiiA depends on the concentration of AHL
**The aiiA and LuxR will have the same degradation rate according to our assumption
*The Lotka-Volterra model is a good representation of our system
<b>ODE (Ordinary Differential Equation)</b>
:::[[Image:2d model 1a.PNG]]
<b>Physical interpretation of the equations</b>
*The production rate of prey is directly proportional to the prey population, i.e. prey will have exponential growth itself. The more number of preys, the more production of preys.
*The death rate of prey is proportional to the product of prey and predator population, i.e. it modeled the death of prey during the encounter of predator
*The production rate of the predator is proportional to the product of prey and predator population, i.e. it modeled the growth of predator when it is fed upon prey.
*The death rate of predator is directly proportional to the predator population, i.e. predator will have exponential decay itself. The more number of predators, the more death of predators occurred.
<b>Comment</b>
*The Lotka-Volterra ODE is probably the simplest prey-predator equations. It allows us to understand the basic feature of prey-predator interaction
*However, this model is too ideal to represent our real system. Further modification might be needed.


= '''Basic Results on the Steady Points and Vector Field''' =
<b>Steady Points</b>
*After analysis, there are two stationary points. (0, 0) & (d/c, a/b)
*The existence of both stationary points is independent of the parameters
*After Jacobian analysis, the stationary point (0, 0) is a saddle point, while (d/c, a/b) is a center
<b>Vector Field</b>


[[Image:Theoretical_Analysis_4b.PNG]]
<font size="4"><b>Vector Field</b></font size="4">
[[Image:Theoretical_Analysis_4c.PNG]]
 
::The previous results help sketch the general allure of the Vector Field :
 
[[Image:Theoretical_Analysis_4b.PNG|thumb|400px|center|Sketch of Vector Field representation of Lotka-Volterra]]  
<br style="clear:both;"/>
 
= '''Closed Trajectories and Neutral Stability''' =
 
 
:*It is easy to prove a very strong result for Lotka-Volterra: once the parameters (a,b,c and d) are set, '''all trajectories''' are not only bounded but '''closed'''.This remarkable result instantly prove that if we start from initial conditions separate from the steady points of the system, then the population of both preys and predators will oscillate.
 
:*However, there is an unwelcome flip side to the result (called neutral stability in Dynamical System Theory).
::Let's imagine that there is an 'accident' such as an unexpected large number of birth of preys at time t (such scenario is realistic in a system like ours due to the intrinsic noise of the system). With the Lotka-volterra dynamic we will then jump to a different (closed) orbit corresponding to the 'accidental' values of  the populations X and Y at time t.
::If there is no other accident we will stay on the new orbit, hence settle on a different oscillatory regime. From an experimental point of view this is unsatisfying since we have no way of predicting the regime when we started the experiment. Furthermore nothing ensures us that the system will not jump again to another orbit.
:*'''Lotka-Volterra is therefore too fatally flawed to be a desirable model for our oscillator'''
 
='''Typical Lotka-Volterra Simulations''' =
<br><br>
[[Image:2d model 1b.PNG|thumb|380px|left|Phase Diagram]]
[[Image:2d model 1c.PNG|thumb|380px|right|Time Diagram]]
<br style="clear:both;"/>
 
:Simulations using different initial conditions are assigned different colors (the open-end of the trajectories is the starting point). In the phase diagram , red dots symbolise a steady points.
<br><br>
:*We can see that the trajectories of Lotka-Volterra are - as expected- closed and spin around the centre steady-point. The nature of the steady point at the origin (it is a saddle point)is visible by the allure of the trajectories at its vicinity ( they are clustered together near the axis and the origin).
:*Furthermore the closer a trajectory is to an axis the larger the amplitude of the trajectory is. Simulations show that for trajectories very close to an axis (say X-Axis) a tiny variation in the initial conditions (or an accidental variation) results in a huge variation in amplitude (and frequency): the Lotka-Volterra is therefore extremely fragile in these regions.
:*Every closed trajectory corresponds to coupled oscillations of the prey and predator populations.
 
='''Control of the Oscillations'''=


= '''Limit cycles''' =
:*Theoretically, we have '''total control over the range of amplitude and frequency of the oscillations'''.
:::[[Image:Theoretical Analysis 1a.PNG]]
::To see this , let's  fix the initial conditions to (Xo,Yo). We can ensure the ratios (d/c and a/b) of the model parameters are such that the centre coincide with (Xo,Yo) and thus we have oscillations of zero amplitude. Now we increase these ratios steadily (the centre moves away from the origin and our initial point), which also increases the amplitude of the oscillations.
*Trajectories will be remain bounded for all the different parameters
::Once we have found an orbit with an amplitude that suits us, we can still modify the parameters so we get any frequency we want. It is straightforward to see that multiplying the parameters of the model (a,b,c and d) by a positive constant does not change the trajectories of the system, only the speed at which they are travelled. Consequently to obtain an oscillation of frequency f1 from an oscillation of frequency f0 it simply takes  to multiply a,b,c and d by f1/f0
<br><br>
:*Thus, we could have oscillations with different amplitudes and frequencies as shown below:


='''Results of Dynamic Analysis''' =
[[Image:2d model 1d.PNG|thumb|400px|center|Comparison with different sets of parameters]]
*2 stationary points, (0, 0) – saddle, (d/c, a/b) center
<br style="clear:both;"/>
:::[[Image:2d model 1b.PNG]]
*From the graph above, we could see that the contours are clustered together near the axis and the
origin; this is due to the saddle nature of the stationary point (origin).
*the contours are also encirclements about a point, which is the second stationary point (center)
*Each encirclement is in fact a periodic oscillation
:::[[Image:2d model 1c.PNG]]
*[http://openwetware.org/images/8/89/Further_analysis_V.pdf Stress analysis] with a given set of parameters
*Or refer to [http://www.openwetware.org/wiki/IGEM:IMPERIAL/2006/project/Oscillator/Modelling/LV here] Section 2 “Back to simplicity” for detail analysis


='''Conclusion'''=
='''Conclusion'''=
<b>Summary of Results</b>
*With a given set of parameters and initial conditions, the result on X-Y plane is a contour around the second stationary point, which is a center.
*Each contour is an enclosed encirclement, i.e. it is a periodic oscillation on its own.
*Any perturbation can drive the oscillation into a different cycle.
*It is especially chaotic if the perturbation is near the origin.
*Hence if possible we should set our second stationary point and initial condition far away from the axis and origin to avoid the drastic change in the output waveform.
<b>Physical Interpretations of Results</b>
*The population of prey and predator oscillated with a certain period and amplitude.
*It is indeed what we expect for the general behaviour of prey-predator interaction


='''Appendices'''=
Lotka-Volterra is a very simple dynamical model for prey-predator interactions. It is very similar in s
<b>Related documents</b>
 
*Stability analysis
Lotka-Volterra is endowed with properties that we hope our system replicates
**Jacobian anaylsis of stationary point for stability of oscillation. click  [http://openwetware.org/images/d/d0/Stability.pdf here] --04/08/06
:- it generates oscillations
**Introduction to analysis of the 2-D ODEs. click [http://openwetware.org/images/e/e7/ODE_analysis.pdf here] --21/08/06
:- by playing on its parameters we can in theory obtain any amplitude and frequency.
*Limit Cycle
 
**Analysis [http://openwetware.org/images/c/c5/Lotka.doc report] of the past progress --31/07/06
However, Lotka-Volterra is also fatally flawed for a system like the one we wish to build as it is far too sensitive to any perturbation/accident/noise. This problem (linked to the concept of neutral stability)can be simply remedied to if we manage to '''build a system with a unique limit-cycle'''.
*Stress Analysis
 
** click [http://openwetware.org/images/d/db/Basic_analysis_for_four_parameters_in_LV_equation.doc here] for the first report --02/08/06<br>
='''Java Applet: Molecular Prey-Predator-System'''=
**click [http://openwetware.org/images/2/29/Further_analysis.pdf here] for the second report --04/08/06<br>
 
**click [http://openwetware.org/images/3/38/Further_analysis_II.pdf here] for the third report --07/08/06<br>
 
**click [http://openwetware.org/images/8/81/Future_analysis_III.pdf here] for the fourth report --07/08/06<br>
**click [http://openwetware.org/images/5/54/Further_analysis_IV.pdf here] for the fifth report --10/08/06<br>
**click [http://openwetware.org/images/8/89/Further_analysis_V.pdf here] for the sixth report --10/08/06<br>
*Java Applet
<HTML>
<HTML>
<HEAD>
<HEAD>
<TITLE>Molecular Prey-Predator-System</TITLE>
<TITLE>Molecular Prey-Predator-System</TITLE>
         <LINK REL="stylesheet" TYPE="text/css" HREF="style.css">
         <LINK REL="stylesheet" TYPE="text/css" HREF="style.css">
</HEAD>
</HEAD>
<BODY>
<BODY>
<H1>Molecular Prey-Predator using JOde</H1>
 
<P><!-- Insert HTML here --><APPLET
<P><!-- Insert HTML here --><APPLET
code="com/rychlik/jode/JOdeApplet.class"
code="com/rychlik/jode/JOdeApplet.class"

Latest revision as of 07:36, 31 October 2006

Model 1: Lotka-Volterra




Introduction

Generalities

  • Lotka Volterra is the earliest (and most famous) population model.
  • It is built upon a pair of first order, non-linear, differential equations, describing the dynamics of ecological systems in which predators and preys interact


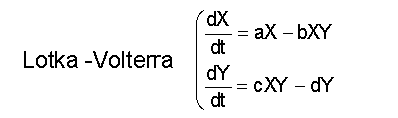
Basic Assumptions of the Model

  • The growth of the prey population X is due to natural reproduction of the preys. In the case of Lotka-volterra the growth is proportional to the population
  • The population of preys is controlled by the hunting carried out by the predators (the natural death rate of the prey is assumed negligible compared to the killing rate due to the predators). In the present case the population decay is proportional to the population of both preys and predators.
  • The predator’s growth is the direct result of hunting the preys. In the present case it is proportional to the population of both preys and predators.
  • Finally the population of the predators is controlled by its natural death (proportional to the population)



Relevance of Lotka-Volterra to the 2D Model

  • The Lotka-Volterra model is probably the simplest prey-predator model and is widely known to yield oscillating populations. It is therefore an ideal candidate as a starting point for our series of analysis.
  • However, it is straightforward to see that the assumptions it is based on are very different from the assumptions of our model. We therefore cannot expect to learn too much about our own system.
  • Furthermore, as we shall see, this model has a critical flaw regarding stability of its oscillations.

Basic Results on the Steady Points and Vector Field

Steady Points

  • The Lotka-Volterra model has two steady points:
- The origin (0, 0)
- (d/c, a/b) (interestingly the steady population of the preys depends only on parameters associated to predators and vice-versa).
  • After Jacobian analysis, it can be shown that the stationary point (0, 0) is a saddle point, while (d/c, a/b) is a centre (that is the vector field will rotate around the point without being attracted or repelled by it).


Vector Field

The previous results help sketch the general allure of the Vector Field :
Sketch of Vector Field representation of Lotka-Volterra


Closed Trajectories and Neutral Stability

  • It is easy to prove a very strong result for Lotka-Volterra: once the parameters (a,b,c and d) are set, all trajectories are not only bounded but closed.This remarkable result instantly prove that if we start from initial conditions separate from the steady points of the system, then the population of both preys and predators will oscillate.
  • However, there is an unwelcome flip side to the result (called neutral stability in Dynamical System Theory).
Let's imagine that there is an 'accident' such as an unexpected large number of birth of preys at time t (such scenario is realistic in a system like ours due to the intrinsic noise of the system). With the Lotka-volterra dynamic we will then jump to a different (closed) orbit corresponding to the 'accidental' values of the populations X and Y at time t.
If there is no other accident we will stay on the new orbit, hence settle on a different oscillatory regime. From an experimental point of view this is unsatisfying since we have no way of predicting the regime when we started the experiment. Furthermore nothing ensures us that the system will not jump again to another orbit.
  • Lotka-Volterra is therefore too fatally flawed to be a desirable model for our oscillator

Typical Lotka-Volterra Simulations



Phase Diagram
Time Diagram


Simulations using different initial conditions are assigned different colors (the open-end of the trajectories is the starting point). In the phase diagram , red dots symbolise a steady points.



  • We can see that the trajectories of Lotka-Volterra are - as expected- closed and spin around the centre steady-point. The nature of the steady point at the origin (it is a saddle point)is visible by the allure of the trajectories at its vicinity ( they are clustered together near the axis and the origin).
  • Furthermore the closer a trajectory is to an axis the larger the amplitude of the trajectory is. Simulations show that for trajectories very close to an axis (say X-Axis) a tiny variation in the initial conditions (or an accidental variation) results in a huge variation in amplitude (and frequency): the Lotka-Volterra is therefore extremely fragile in these regions.
  • Every closed trajectory corresponds to coupled oscillations of the prey and predator populations.

Control of the Oscillations

  • Theoretically, we have total control over the range of amplitude and frequency of the oscillations.
To see this , let's fix the initial conditions to (Xo,Yo). We can ensure the ratios (d/c and a/b) of the model parameters are such that the centre coincide with (Xo,Yo) and thus we have oscillations of zero amplitude. Now we increase these ratios steadily (the centre moves away from the origin and our initial point), which also increases the amplitude of the oscillations.
Once we have found an orbit with an amplitude that suits us, we can still modify the parameters so we get any frequency we want. It is straightforward to see that multiplying the parameters of the model (a,b,c and d) by a positive constant does not change the trajectories of the system, only the speed at which they are travelled. Consequently to obtain an oscillation of frequency f1 from an oscillation of frequency f0 it simply takes to multiply a,b,c and d by f1/f0



  • Thus, we could have oscillations with different amplitudes and frequencies as shown below:
Comparison with different sets of parameters


Conclusion

Lotka-Volterra is a very simple dynamical model for prey-predator interactions. It is very similar in s

Lotka-Volterra is endowed with properties that we hope our system replicates

- it generates oscillations
- by playing on its parameters we can in theory obtain any amplitude and frequency.

However, Lotka-Volterra is also fatally flawed for a system like the one we wish to build as it is far too sensitive to any perturbation/accident/noise. This problem (linked to the concept of neutral stability)can be simply remedied to if we manage to build a system with a unique limit-cycle.

Java Applet: Molecular Prey-Predator-System

<html> <HEAD>

<TITLE>Molecular Prey-Predator-System</TITLE> 

       <LINK REL="stylesheet" TYPE="text/css" HREF="style.css">

</HEAD> <BODY>

<P><!-- Insert HTML here --><APPLET code="com/rychlik/jode/JOdeApplet.class" NAME="JOde" width=650 height=750 archive="http://openwetware.org/images/a/a3/JOdeApplet.jar" mayscript="true"> <PARAM NAME="isframed" VALUE="false"> <PARAM NAME="background" VALUE="c0c0c0"> <PARAM NAME="autonomous" VALUE="true"> <PARAM NAME="min1" VALUE="0"> <PARAM NAME="max1" VALUE="100"> <PARAM NAME="min2" VALUE="0"> <PARAM NAME="max2" VALUE="30"> <PARAM NAME="variable0" VALUE="t"> <PARAM NAME="equation0" VALUE=" a = 1;b = 0.1;c = 0.02;d = 0.5"> <PARAM NAME="variable1" VALUE="X"> <PARAM NAME="variable2" VALUE="Y"> <PARAM NAME="equation1" VALUE="a*X-b*X*Y "> <PARAM NAME="equation2" VALUE="c*X*Y-d*Y"> 

       <PARAM NAME="initconds" VALUE="40,15;10,5">

<PARAM NAME="showinitconditions" VALUE="true"> <PARAM NAME="showpoints" VALUE="false"> <PARAM NAME="showslopes" VALUE="true"> <PARAM NAME="showaxes" VALUE="true"> <PARAM NAME="minparameter" VALUE="0"> <PARAM NAME="maxparameter" VALUE="2000"> <PARAM NAME="parametersegments" VALUE="20000"> <PARAM NAME="algorithm" VALUE="RK4"> <PARAM NAME="label" VALUE="Molecular Prey-Predator"> </APPLET> </P>

a = 1;b = 0.1;c = 0.02;d = 0.5

Instructions on using the JOde Applet</A></EM></P> <P>Using the applet written by: <A HREF="http://alamos.math.arizona.edu/">Marek Rychlik</A> </BODY> </html>

Retrieved from "https://openwetware.org/mediawiki/index.php?title=IGEM:IMPERIAL/2006/project/Oscillator/Theoretical_Analyses/Results/2D_Model1&oldid=84250"