IGEM:IMPERIAL/2006/project/Oscillator/Theoretical Analyses/Results/2D Model3

Model 3: Bounded Predator and Prey Growth

Introduction

Generalities

• Bounding the growth term for the preys moves us further from our goal of creating oscillations as it stabilises the system too much.
• We now seek to counteract this by also bounding the growth of the predators.

Physical interpretation of the equations

• All the arguments that bounded the growth of the preys apply to the predators (production is limited by the number of promoters as well). This results in a Michaelis-Menten-like kinetics.
• For all the degradation terms of the system the assumptions made for Lotka-Volterra remain.

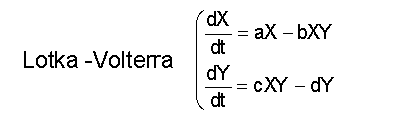
Dimensionless Version of the System

• The complexity of system has increased notably (6 independent parameters) so much so that direct symbolic computation with Matlab is not available.
• We therefore normalised the system before analysing it - thus reducing the number of free parameters.
• Normalisation was achieved by changing the scale reference on the X and Y axes as well as in time. Therefore the behaviour of a system is unchanged by normalisation.
• After normalisation the system only has 3 free parameters

Basic Results on the Steady Points and Vector Field

• The dynamic analysis of the system yields results that are very similar to the previous system where only the growth of preys was bounded.

• The system has two stationary points
• The first stationary point (0, 0) is a saddle point
• The second stationary point (coordinates) is always stable

• The Vector Field is again reminiscent of Lotka-Volterra (if only even more distorted).

Behaviour at Infinity

• We get again similar results to those obtained for the bounded prey growth.

• The trajectories remain bounded as time goes to infinity regardless of the choice of parameters.

- We can therefore apply Poincare-Bendixson's theorem.

- Because the system only has 2 steady points , one a saddle point the other a stable point we are sure the system will not oscillate.

- For initial conditions (Xo,Yo) both non-null the trajectories will converge to the stable steady point

Typical Simulations

• Preliminary Note on the Simulations:

As with the previous models, simulations using different initial conditions are assigned different colors (the open-end of the trajectories is the starting point). Finally in the phase diagrams , red dots symbolise a steady points.

• The typical behaviour of the system (convergence to stable steady point)
• The corresponding time variations of the prey and predator populations are dampened oscillations:

Phase Diagram

Time Diagram

Conclusion

The bounding of the predator growth had a dramatic effect on the system and broke the balance between the growth terms of the preys and predators and their decay/degradations terms. Our attempt to re-balance the system by bounding the growth of the predators has failed to yield any oscillation. This suggests that a better way to re-balance the system is to balance the growth and decay terms of the preys and/or predators instead.

Appendices

Related documents

• Stability analysis