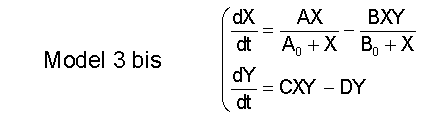IGEM:IMPERIAL/2006/project/Oscillator/Theoretical Analyses/Results/2D Model3a: Difference between revisions

From OpenWetWare
Jump to navigationJump to search
No edit summary
 
(22 intermediate revisions by 2 users not shown)
Line 1: Line 1:
2D Model 3: Bounded Predator and Prey Growth
<br><br>
<font size="6"><center>'''Model 3 bis: Bounded Predator and Prey Growth'''</center></font size="6">
<br><br><br>


= '''Introduction''' =
= '''Introduction''' =
<font size="4">'''Generalities''' </font size="4">
:*The analysis of the model with bounded growth terms for both preys and predators has hinted that in order to get oscillations it was more important to balance the respective growth and decay terms of a population than to balance the growth terms within the whole system (the idea being to achieve some form of control of the ratios of the populations).
:*We now test the validity of this interpretation by bounding both growth and decay of the preys while leaving the terms relating to the predators identical to those in the Lotka-Volterra model.


Bounding the growth term for the preys moves us further from our goal of creating oscillations as it stabilises the system too much. We now seek to counteract this by also bounding the growth of the predators.
:::[[Image: LV3bis.png|center]]


<b>Physical interpretation of the equations</b>
<font size="4">'''Physical interpretation of the equations'''</font size="4">
* All the arguments that bounded the growth of the preys apply to the predators (production is limited by the number of promoters as well). This results in a Michaelis-Menten-like kinetics.  
:* All the arguments that bounded the growth of the preys still apply (production is limited by the number of promoters).
* For all the degradation terms of the system the assumptions made for Lotka-Volterra remain.
:* The decay term of the preys is due to an enzymatic reaction, typically modelled with a Michaelis-Menten kinetics.  
:* For all the predator terms of the system (second differential equation) we make the same assumption as with Lotka-Volterra that is:
::- The predator’s growth is the direct result of interacting the preys.
::- In the present case it is proportional to the population of both preys and predators.
::- The population of the predators is controlled by its natural death (proportional to the population)
<br><br>


<b>ODE (Ordinary Differential Equation)</b>
= '''Basic Results on the Steady Points''' =


:::[[Image: Theoretical_Analysis_6h.PNG]]
: The dynamic analysis of the system yields results that '''differ from the previous system''' in a significant way:
 
:* The system has two stationary points
 
:* The first stationary point (0, 0) is a saddle point
 
:* The second stationary point ( Xs=D/C, Ys=A(Bo+Xs)/(B(Ao+Xs)) ) is '''not''' always stable
<b>Dimensionless Version of the System</b>
:* The nature of the second steady point depends on the respective values of Ao and Bo:
 
::- if Ao>Bo, the point is '''stable''' (it attracts all the trajectories in its vicinity)
The complexity of system has increased notably (6 independent parameters) so much so that direct symbolic computation with Matlab is not available. We therefore normalised the system before analysing it - thus reducing the number of free parameters. Normalisation was achieved by changing the scale reference on the X and Y axes as well as in time. Therefore the behaviour of a system is unchanged by normalisation. 
::- If Ao=Bo, the point is a '''centre''' (the trajectories in its vicinity spin around it)
After normalisation the system only has 3 free parameters
::- if Ao<Bo, the point is '''unstable''' (it attracts all the trajectories in its vicinity)
 
= '''Basic Results on the Steady Points and Vector Field''' =
 
The dynamic analysis of the system yields results that are '''very similar''' to the previous system where only the growth of preys was bounded.
* The system has two stationary points
* The first stationary point (0, 0) is a saddle point
* The second stationary point (coordinates) is always stable
 
The Vector Field is again reminiscent of Lotka-Volterra (if only even more distorted).


= '''Behaviour at Infinity''' =
= '''Behaviour at Infinity''' =


We get again similar results to those obtained for the bounded prey growth.
:The '''trajectories remain bounded''' as time goes to infinity regardless of the choice of parameters.
 
:* We can therefore apply Poincare-Bendixson's theorem.  
The trajectories remain bounded as time goes to infinity regardless of the choice of parameters.
:* Due to the saddle point nature of the origin (0,0)
:- We can therefore apply Poincare-Bendixson's theorem.  
::- any trajectory starting on the Y-axis will be attracted to  the origin
:- Because the system only has 2 steady points , one a saddle point the other a stable point we are sure the system will not oscillate.
::- any trajectory starting on the X-axis will be repelled to infinity
:- For initial conditions (Xo,Yo) both non-null the trajectories will converge to the stable steady point
:* For initial conditions (Xo,Yo) both non-null the trajectories will converge
::- to the stable steady point if Ao>Bo
::- else (Ao<=Bo) to a '''Limit Cycle''': We have '''Oscillations'''


='''Typical Simulations''' =
='''Typical Simulations''' =
* The typical behaviour of the system (convergence to stable steady point) can be illustrated by the following simulation:
:::[[Image:2d model 3b.PNG]]


* The corresponding time variations of the prey and predator populations are dampened oscillations:
<font size="4">'''First Case: Stable System'''</font size="4">
:::[[Image:2d model 3c.PNG]]
:The first typical behaviour of the system (convergence to stable steady point) can be illustrated by the following phase diagram, and the corresponding time variations of the prey and predator populations (dampened oscillations)
<br><br>
[[Image:2d model 3a1.PNG|thumb|380px|left|Phase Diagram]]
[[Image:2d model 3a2.PNG|thumb|380px|right|Time Diagram]]
<br style="clear:both;"/>
<br><br>
<font size="4">'''Second Case: Oscillations'''</font size="4">
:The second typical behaviour of the system (Oscillations around a limit cycle) can be illustrated by the following phase diagram , and the corresponding time variations of the prey and predator populations (oscillations)
<br><br>


='''Conclusion'''=
[[Image:2d model 3a3.PNG|thumb|380px|left|Phase Diagram]]
[[Image:2d model 3a4.PNG|thumb|380px|right|Time Diagram]]
<br style="clear:both;"/>


The bounding of the predator growth had a dramatic effect on the system and broke the balance between the growth terms of the preys and predators and their decay/degradations terms.
'''Note on the Simulations'''
Our attempt to re-balance the system by bounding the growth of the predators has failed to yield any oscillation.
:As with the previous models, simulations using different initial conditions are assigned different colors (the open-end of the trajectories is the starting point). In the phase diagrams , red dots symbolise a steady points.
This suggests that a better way to re-balance the system is to balance the growth and decay terms of the preys and/or predators instead.
<br><br>
 
<font size="4"> '''Control of the Oscillations'''</font size="4">
='''Appendices'''=
:We obtained results that are very similar to the case of Lotka-Volterra:
<b>Related documents</b>
::- By playing on the ratios D/C and B/A we can push the second steady point far away from the origin, which has the desired effect of increasing the size of the limit cycle - and its amplitude
*Stability [http://openwetware.org/images/1/17/MM_model_analysis_3.doc analysis]
::- Once a cycle of desired amplitude its frequency can be changed by multiplying A,B,C and D by a positive constant.


='''Conclusion'''=


:::[[Image:2d model 3y.PNG]]
*The bounding of the predator growth had a dramatic effect on the system and broke the balance between the growth terms of the preys and predators and their decay/degradations terms.  
:::[[Image:2d model 3z.PNG]]
*Our attempt to re-balance the system by bounding the growth and decay of the preys has succeeded in  yielding '''oscillations'''.
*Furthermore we have '''total control over the amplitude and frequency''' of the oscillations.

Latest revision as of 07:38, 31 October 2006



Model 3 bis: Bounded Predator and Prey Growth




Introduction

Generalities

  • The analysis of the model with bounded growth terms for both preys and predators has hinted that in order to get oscillations it was more important to balance the respective growth and decay terms of a population than to balance the growth terms within the whole system (the idea being to achieve some form of control of the ratios of the populations).
  • We now test the validity of this interpretation by bounding both growth and decay of the preys while leaving the terms relating to the predators identical to those in the Lotka-Volterra model.

Physical interpretation of the equations

  • All the arguments that bounded the growth of the preys still apply (production is limited by the number of promoters).
  • The decay term of the preys is due to an enzymatic reaction, typically modelled with a Michaelis-Menten kinetics.
  • For all the predator terms of the system (second differential equation) we make the same assumption as with Lotka-Volterra that is:
- The predator’s growth is the direct result of interacting the preys.
- In the present case it is proportional to the population of both preys and predators.
- The population of the predators is controlled by its natural death (proportional to the population)



Basic Results on the Steady Points

The dynamic analysis of the system yields results that differ from the previous system in a significant way:
  • The system has two stationary points
  • The first stationary point (0, 0) is a saddle point
  • The second stationary point ( Xs=D/C, Ys=A(Bo+Xs)/(B(Ao+Xs)) ) is not always stable
  • The nature of the second steady point depends on the respective values of Ao and Bo:
- if Ao>Bo, the point is stable (it attracts all the trajectories in its vicinity)
- If Ao=Bo, the point is a centre (the trajectories in its vicinity spin around it)
- if Ao<Bo, the point is unstable (it attracts all the trajectories in its vicinity)

Behaviour at Infinity

The trajectories remain bounded as time goes to infinity regardless of the choice of parameters.
  • We can therefore apply Poincare-Bendixson's theorem.
  • Due to the saddle point nature of the origin (0,0)
- any trajectory starting on the Y-axis will be attracted to the origin
- any trajectory starting on the X-axis will be repelled to infinity
  • For initial conditions (Xo,Yo) both non-null the trajectories will converge
- to the stable steady point if Ao>Bo
- else (Ao<=Bo) to a Limit Cycle: We have Oscillations

Typical Simulations

First Case: Stable System

The first typical behaviour of the system (convergence to stable steady point) can be illustrated by the following phase diagram, and the corresponding time variations of the prey and predator populations (dampened oscillations)



Phase Diagram
Time Diagram




Second Case: Oscillations

The second typical behaviour of the system (Oscillations around a limit cycle) can be illustrated by the following phase diagram , and the corresponding time variations of the prey and predator populations (oscillations)



Phase Diagram
Time Diagram


Note on the Simulations

As with the previous models, simulations using different initial conditions are assigned different colors (the open-end of the trajectories is the starting point). In the phase diagrams , red dots symbolise a steady points.



Control of the Oscillations

We obtained results that are very similar to the case of Lotka-Volterra:
- By playing on the ratios D/C and B/A we can push the second steady point far away from the origin, which has the desired effect of increasing the size of the limit cycle - and its amplitude
- Once a cycle of desired amplitude its frequency can be changed by multiplying A,B,C and D by a positive constant.

Conclusion

  • The bounding of the predator growth had a dramatic effect on the system and broke the balance between the growth terms of the preys and predators and their decay/degradations terms.
  • Our attempt to re-balance the system by bounding the growth and decay of the preys has succeeded in yielding oscillations.
  • Furthermore we have total control over the amplitude and frequency of the oscillations.
Retrieved from "https://openwetware.org/mediawiki/index.php?title=IGEM:IMPERIAL/2006/project/Oscillator/Theoretical_Analyses/Results/2D_Model3a&oldid=84256"