Physics307L:People/Muehlmeyer/Formal

Measuring the Speed of Light

Author: Justin Muehlmeyer

Experimentalists: Justin Muehlmeyer and Alexander Barron

University of New Mexico

Department of Physics and Astronomy Junior Lab November 2008

jmuehlme@unm.edu

Abstract

To approximate the speed of light we measured the "flight time" of pulses of light emitted by a light emitting diode by measuring the time difference between LED emission and PMT reception of the light signal down a tube via a time amplitude convertor (TAC). By varying the distance the light signal travels we plot distance vs. flight time and use the linear-least squares method to approximate the slope of our data, which gives us the speed of light. We found that our best approximation to the accepted value of 2.99 X 10⁸ m/s was 2.94 X 10⁸ m/s, which came from large variations in distance and from using the "time walk" correction that accounts for the changing intensity of the light as the LED distance approaches the PMT.

Materials and methods

Instrumentation

• PMT: Perfection Mica Company N-134

• Digital Oscilloscope: Tektronics TDS 1002

• LED: Cycles on and off at around 10KHz depending on the voltage applied. Recommended voltage is around 200 volts DC.

• LED Power Supply:

• PMT Power Supply:

• Cardboard tube wide enough to fit the PMT on one end and LED on the other.

• 2 Polarizing filters: one for the PMT, one for the LED.

Set Up

A long cardboard tube has the LED on one end pointing in at the PMT receiving its signals on the other end. The LED is strapped to 3 meter sticks binded by tape so that we can push the LED down the tube and measure the change in distance from its initial point. The PMT and LED each have a polarizer attached to their fronts, so that as we push the LED in we can rotate the PMT on the other end to maintain a constant intensity (see segment on intensity and time walk below). The anode of the PMT is connected to the input on the delay module and to channel 1 of the oscilloscope.

The LED is connected to its power supply via a BNC cable. We have the LED power supply outputing 190 V. The PMT is connected via a BNC to its high voltage source outputing at 1900 V.

To measure the time difference between LED emission and PMT reception we have a time amplitude converter (TAC) which converts the time difference of its inputs into a voltage that is proportional to that time difference. The two BNC inputs are labeled the "start" time from LED emission, and the "stop" time from PMT reception through the delay module. The output ratio of the time difference between the two inputs is 10 V = 50 nS, which we read on the digital oscilloscope in channel 2.

Time Walk

Since our TAC triggers at a fixed voltage, its triggering time occurs later for small incoming amplitudes then larger ones. This creates an issue because as we push the LED in closer to the PMT, the PMT signal increases in amplitude and the "time walk" problem then becomes a large source of systematic error. To avoid this issue we must maintain a constant PMT signal by using the polarizers to maintain constant intensity on the PMT.

The intensity was kept constant by rotating the PMT by slight amounts which rotated the polarizer covering its "lens". The polarizer "filters" or "cuts" the incoming light's electric field based on the angle that the polarizer film molecules are aligned. There is a point (or angle rather) when the polarizer cuts the incoming light entirely, and no voltage can be seen from he TAC at all. This means the alignment of the polarizer with the incoming electric field from the LED is perindicular. This is found to be of great importance, if we don't maintain a constant intensity for the PMT reception then our actual time difference will be scewed due to the fact that the TAC is receiving more signals from the PMT then it should.

Procedure

We varied the distance between the LED module and the photomultiplier tube, taking voltage measurements from the oscilloscope.

We used two methods to read the data on the oscilloscope. The raw signal from the TAC when the oscilloscope is in "sample" mode is very turbulent and quite impossible to read. We first used the cursors to eye an average, then with the second cursor we eyed the deviations from this average. This was time consuming, and somewhat frustrating due to the extreme variations of the signal. Then we remembered that the oscilloscope can do the averaging for us.

Setting the oscilloscope data acquisition mode to "average", the oscilloscope does all the work for us. Over a period of time it takes an average and displays it. Therefore the signal we see is actually delayed from the actual input but is a better representation. So we decided to take all of our data using the "measure" function on the oscilloscope when the data acqusition mode was on "average". This of course is an easier way of doing it, and we took all of our data later using the measure function for efficiency sake. The measure function does not read the deviation however, so this value had to be eyed based on the fluctations of the signal from that average.

Plotting the distance vs. time and taking the slope of the line best fit line of these points via the least-squares method produced an estimate for the speed of light. Please see our data below.

Data and Analysis

Data

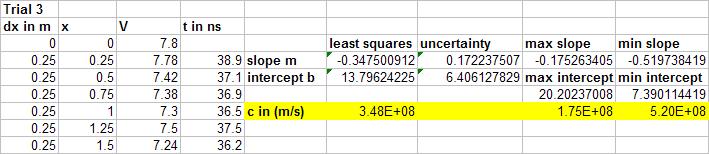
We did four trials, each with different changes in distance, and the last to see the importance of the time walk correction:

Trial 1 distance changes increased rapidly from the initial point.

Trial 2 was to see what small changes in distances would give.

Trial 3 was for large changes in distance, but not as large as trial 1.

Trial 4 was to check the importance of time walk correction. We did not use the polarizers here to correct for the changing intensity.

Analysis

[math]\displaystyle{ A=\frac{\sum x_i^2 \sum y_i - \sum x_i \sum x_i y_i}{\Delta_{fixed}} }[/math] [math]\displaystyle{ \mbox{,}~~~~~~~~~~~~~~~~~ \sigma_a^2 = \frac{\sigma_y^2}{\Delta_{fixed}} \sum x_i^2 }[/math]

[math]\displaystyle{ B=\frac{N\sum x_i y_i - \sum x_i \sum y_i}{\Delta_{fixed}} }[/math] [math]\displaystyle{ \mbox{,}~~~~~~~~~~~~~~~~~ \sigma_b^2 = N \frac{\sigma_y^2}{\Delta_{fixed}} }[/math] (I believe this is the same as 1/N * σ_y² / σ_x², where σ_x² is the population variance of the experimental x values (not the variance of an individual x measurement)

[math]\displaystyle{ \Delta_{fixed}=N \sum x_i^2 - \left ( \sum x_i \right )^2 }[/math] (This is actually N² times the population variance of x...not sure if that helps in any kind of understanding, though.)

[math]\displaystyle{ \sigma_y }[/math] can be inferred from the chi-squared value and the number of degrees of freedom. If you have an independent estimate of [math]\displaystyle{ \sigma_y }[/math] (e.g. SEM of several indpendent measurements), this should be consistent with the inferred uncertainty. LINEST (excel linear fitting) uses the implied value for calculating the uncertainty of the fit parameters.

[math]\displaystyle{ \sigma_{y~implied}^2 = \frac {1}{N-2} \sum (y_i - A - Bx_i)^2 }[/math] [math]\displaystyle{ \mbox{,}~~~~~~~\mbox{recall,}~~ \chi^2 = \frac {1}{\sigma_y^2} \sum (y_i - A - Bx_i)^2 }[/math]

Results and Analysis