The Project's Description
The Project's Description
The Overview of DNAmazing Program
DNAmazing program consists of three main modules: the Design, GUI, and Computational Chemistry toolkits.
The programming language is C# and the integrated development environment (IDE)is Microsoft Visual Studio 2010.
The Design is the backbone of the program which provides basic functions of a DNA Origami design tool: receiving information about the DNA Origami structures (shapes, sticky ends) and returning the necessary information of staple and scaffold sequences to synthesize the structures in labs.
The Computational Chemistry toolkits (general description here)
The GUI will provide users with basic interface with the program to (general description here)
The Design
Basic Dogmas of Design
The Design of 2D DNA Origami in DNAmazing follows the principles which were laid out in Rothermund's first paper in 2006. The basic idea of DNA Origami is to fold a DNA helix into a desired shape. One strand of the DNA helix is a long and continuous DNA strand, called the scaffold strand; another strand consists of several short DNA fragments, the staple strands. The staple strands are together complementary to the scaffold to form the DNA helix. The formation of crossovers of staple stands keep the scaffold strand in the desired shape.

For the purpose of design, the folded DNA helix is conceptually divided into several small helices which one helix is one turn of the folded helix. Each of these turns/helices is represented as one square in the program. Each square is given a number. The labeling is done from the left to right and from the bottom row to the top row. The non-integer number of bases pair per turn: 10.67 will be approximated as 11 base pairs. The DNA helix is folded by forming several crossovers in the staple strands; these crossovers indicate the positions where a staple strand switch to another helix located on a different row. These switching only occurs at locations where DNA twist places at its tangent point between helices which is apart by any odd number of half-turns. In this project, we will stick to 1.5 turns.
Throughout the software, there are 2 coordinate systems which are used to refer a specific square in the DNA Origami structures. The labeling mentioned in this part is the matrix coordinate. The other is the scaffold coordinate which will be described later in 6.2.3 Generation of scaffolding pathways.
Inputting parameters
Recognizing the fact that the conventional input of existing programs may not be convenient for large and complex structures,DNAmazing adopts a very different way: a lithography-like way.Instead of drawing the scaffold way, which may be painful and even impossible for complicated designs,users will input the dimensions of a rectangle that encloses their desired structure. The dimensional units are the number of helices/squares per row and per column. The users will achieve their final desired shape by eliminate the unwanted squares. The elimination id done by inputting the number of the unwanted squares (null squares).
In the above example, the desired DNA Origami shape is enclosed by a rectangular frame 6 squares x 6 squares. There are totally 8 null squares: 12,18,,24,30,17,23,29,35.
Generation of scaffolding pathways
One of the unique features of DNAmazing is its ability to automatically generate the scaffolding pathways. For the existing programs, users have to manually design how to fold a scaffold strand to the desired shapes. This progress may be tedious for complex structures such as smiling faces in Rothermund's paper. In DNAmazing, users only have to conceptualize the DNA Origami structures into series of squares which was described in the previous part. This is definitely more relaxing.
Basically, the process of generation of scaffolding is to thread the scaffold strand to all the squares that each square is visited only once. This is very similar to the algorithm of the Hamiltonian circuit (or the Hamiltonian path). In graph theory, a Hamiltonian circuit is a path in an undirected graph that visits each vertex exactly one. Another example of Hamiltonian circuit is the problem of a business man to visit all the cities only once to deliver goods.
Each normal square in DNA Origami is modeled as a vertex which can be linked to its 4 adjacent neighbors in four directions, but not diagonal neighbors. The null squares are isolated squares and there should not be any links to them. The scaffolding path starts with the first square and extend by adding one of 4 neighbors of the first square. A Hamiltonian circuit can be solved by exploring all the possible paths that satisfy the condition.The process is repeated until it can no longer extend because of there are not any possible choices or the path has passed through all squares. If the latter happens, the process is done and the scaffolding pathway is generated successfully. In the former cases, the program will take one step back and explore other choices.
By using the algorithm of Hamiltonian circuit, DNAmazing is able to find all the possible scaffold ways. However, not all of these ways are reasonable for the DNA Origami. A filter must be included to select the paths which are suitable for DNA Origami. Below are some rules which we use in the filtering process:
- The first square is either square 0 or the square at the middle of the first row
- If the first square is square 0, the scaffolding pathway should run continuously and only turn over to another row at either two ends.If the first square is the middle of the first row, the last square in the scaffold way must be on the right of the first square.
- The scaffold should not run in the vertical direction.
The result of this stage is a 1D matrix containing the ordinal numbers of the squares that the scaffold passes through. For instance,the scaffold way in the above figure will be presented as C=[2,1,0,6,7,8,14,13,19,20,26,25,31,32,33,34,28,27,21,22,16,15,9,10,11,5,4,3]
Determination of crossover positions
The next step in the Design part is the determination of crossover positions. Crossovers are places where the staples switch to another helix located on a different row. The crossovers are crucial to the folding of the scaffold strand. In fact, they are the only forces which prevent the scaffold from unfolding in a process of achieving higher entropy (more disordered) and thus lower ΔG. The basic principle to determine the positions of crossovers was laid out by Rothermund: the spacing between crossovers in 2D DNA Origami structures must be an odd number of half turns. In other words, 2 vertically adjacent staples meet at their tangent points every an odd number of half turn. Thus, the staples will be in the least strained state at the crossovers. Particularly, in this project, we will stick to 1.5 turns as the unit for the spacing of crossovers.
The algorithm to determine the crossover positions starts with the generation of an ArrayList, which is elementally a matrix with flexible dimensions. We named it PosCros. The Poscros Arraylist is used to add the squares which contain the crossover position. The first element of PosCros is always the first element in the scaffold way. The next elements are determined based on in which category the previous element is; the categorization is done based on the relative distance between the element and the closest turning point of the scaffold.
Addition of sticky ends
Sticky ends serving as an extra ends of a staples should not interfere with the scaffold folding in the formation of DNA Origami. So, sticky end sequences must not have any stable binding to any sequence in the scaffold. To generate sticky end sequences, DNA sequences of a defined length are generated randomly. The newly generated sequences are then to be examined for its ability to bind to the scaffold. Sequences which have a rather stabilizing binding with any position in the scaffold are discarded. Only those without stable scaffold binding are kept and can be used as sticky ends’ sequences.
To determine if the sticky end would have any stabilizing binding to the scaffold, one needs to know binding energy of the sticky end to every sequence in the scaffold. In addition, a threshold below which the binding is considered stable is also required.
Calculation of binding energy
The Sticky end sequence given is mapped along the scaffold length and the binding energy (deltaG) is calculated for each match/mismatch binding. The calculation was done using the formula and complete thermodynamic database for internal single mismatches discussed in SantaLucia’s studies (2006) (1). The formula and parameters are shown bellow:
Nearest-neighbor [math]\displaystyle{ \Delta G^o }[/math] increments (kcal/mol) for internal single mismatches next to Watson-Crick pairs in 1 M NaCl
For example, consider the total binding energy of following DNA duplex. The mismatch base pair is bold:
Set up a threshold
To determine if the mismatched complement between the sticky ends and the scaffolds are stable or unstable, a threshold of binding energy ([math]\displaystyle{ \Delta G^o }[/math]) is required. Binding energy less than or equal to this threshold would be consider stable. There should not be an absolute threshold value for every DNA sequence with different length. Longer DNA sequences require lower [math]\displaystyle{ \Delta G^o }[/math] for a stable binding. Therefore, the threshold is set up as a variable calculated based on the sequence length: Let n be the length of DNA sequence. If n is even, the threshold is calculated as follow:
if n is odd, then the formula for the threshold is:
In the equation, -0.58 is the binding energy between 5’-TA-3’/3’-AT-5’, and -0.88 is the binding energy between 5’-AT-3’/3’-TA-5’. This means that the right side of the equation equal the binding energy of the complement 5’-(AT)n-3’/3’-(TA)n-5’of the same length. In other words, there would be no binding between the sticky end and scaffold which is more stable than the least stable Watson-Crick fully complemented DNA duplex
Merging Process
The prediction of the thermal stability of the duplex produced from sticky end
Predict the thermal stability of short DNA duplex which is formed upon the binding of the sticky end and its complementary single-stranded strand.
The capability to estimate the thermal stability will aid in numerous applications such as (i) predicting the stability of a local sequence on DNA duplex, or of a probe-gene complex, (ii) calculating the melting temperatures of short sequences in hybridization experiments, (iii) determining the optimal length of the probe oligomer to produce stable duplexes with the sticky ends. Recently, the order-disorder transition of a sticky end with its complementary single strand is also important in controlling the dynamic movement of nanomotors, which are made from DNA strands (reference?).
Research has shown that the thermal stability of duplex is affected by sequence information and base compositions. However, the sequence of DNA strand is the major determinant of [math]\displaystyle{ \Delta }[/math][math]\displaystyle{ H^o }[/math], [math]\displaystyle{ \Delta }[/math][math]\displaystyle{ S^o }[/math], and [math]\displaystyle{ \Delta }[/math][math]\displaystyle{ G^o }[/math]. We apply the nearest-neighbor (NN) method to determine the transition enthalpy, entropy, free energy, and melting point of short DNA duplex. This method calculates those thermodynamic values using the stacking interaction between Watson-Crick neighboring bases in the DNA strands.
DNAmazing program will not only assist in random generating stick ends attached to pre-determined positions on DNA Origami, but also allow users to input their preferred sequence information of the sticky ends. Since different sequences have different thermal stability (represented by [math]\displaystyle{ \Delta }[/math][math]\displaystyle{ H^o }[/math], [math]\displaystyle{ \Delta }[/math][math]\displaystyle{ S^o }[/math], and [math]\displaystyle{ \Delta }[/math][math]\displaystyle{ G^o }[/math]) upon binding, knowing those thermodynamic values is crucial to study the function and applications of the sticky ends.
Besides, DNAmazing program also helps to determine whether the sticky end's sequence input by user is complementary to the scaffold strand or other staple strands.
There are many groups have dedicated researching on NN method to determine [math]\displaystyle{ \Delta }[/math][math]\displaystyle{ H^o }[/math], [math]\displaystyle{ \Delta }[/math][math]\displaystyle{ S^o }[/math], [math]\displaystyle{ \Delta }[/math][math]\displaystyle{ G^o }[/math], and [math]\displaystyle{ T_m }[/math] of short DNA oligomers and have arrived on the same formula as demonstrated below. However, since difference researches used different starting materials (short DNA oligomers, polymers, etc.), the values for one parameter slightly vary. We have chosen the latest results obtained by John S.L. et al to incorporate into our software.
- [math]\displaystyle{ \Delta H^o_{} = \Delta H^o_{ini} + \Delta H^o_{sym} + \Delta H^o_{AT term.} + \Sigma \Delta H^o_{stacking}\! }[/math]
Where [math]\displaystyle{ \Delta H^o_{} }[/math] is the helix initiation enthalpy of the transition process; [math]\displaystyle{ \Delta H^o_{sym} }[/math] is the symmetry term only applies to self-complementary duplexes, accounting for the enthalpy difference between a duplex formed from a self-complementary sequence and a duplex formed from 2 complementary strands; [math]\displaystyle{ \Delta H^o_{AT term.} }[/math] is applied for each end of a duplex that has a terminal AT, accounting for the end-fraying caused by AT base pair; [math]\displaystyle{ \Sigma \Delta H^o_{stacking} }[/math] is the total of enthalpy of propagation step in the sequence.
For example:
- [math]\displaystyle{ \begin{align} \Delta H^o_{} (5'-CGTTGA-3') & = \Delta H^o_{ini} + \Delta H^o_{sym} + \Delta H^o_{AT term.} + \Sigma \Delta H^o_{stacking} \\ & = 0.2 + 0.0 + 2.2 + ( - 10.6 - 8.4 - 7.6 - 8.5 - 8.2) \\ & = -40.9 (kcal/mol) \\ \end{align} }[/math]
[math]\displaystyle{ \Delta S^o }[/math], [math]\displaystyle{ \Delta G^o }[/math] are calculated using the same formula (1) above.
There are 10 propagation steps, 1 initiation, and 1 terminal AT correction to make up a total of 12 NN parameters shown in Table 1. These values are obtained via multiple linear regression of the results from differential scanning calorimetry (DSC) of 108 short DNA sequences.
| Propagation step | [math]\displaystyle{ \Delta H^o }[/math] (kcal/mol) | [math]\displaystyle{ \Delta S^o }[/math] (e.u.) | [math]\displaystyle{ \Delta G^o }[/math] (kcal/mol) |
|---|---|---|---|
| AA/TT | -7.6 | -21.3 | -1.00 |
| AT/TA | -7.2 | -20.4 | -0.88 |
| TA/AT | -7.2 | -21.3 | -0.58 |
| CA/GT | -8.5 | -22.7 | -1.45 |
| GT/CA | -8.4 | -22.4 | -1.44 |
| CT/GA | -7.8 | -21.0 | -1.28 |
| GA/CT | -8.2 | -22.2 | -1.30 |
| CG/GC | -10.6 | -27.2 | -2.17 |
| GC/CG | -9.8 | -24.4 | -2.24 |
| GG/CC | -8.0 | -19.9 | -1.84 |
| Initiation | +0.2 | -5.7 | +1.96 |
| Terminal AT penalty | +2.2 | +6.9 | +0.05 |
| Symmetry correction | 0.0 | -1.4 | +0.43 |
The melting point of short DNA chain, defined as the temperature at which half of double-stranded DNA sequences have dissociated, is calculated as following:
- [math]\displaystyle{ T_m = \frac{\Delta H^o \times 1000} {\Delta S^o + R \times \ln( \frac{C_t}{x} ) - 273.15} }[/math]
where [math]\displaystyle{ C_t }[/math] is the total molar strand concentration. For nonself-complementary duplexes x=4, and for self-complementary, x=1.
NN method is just an approximation because it neglects the secondary interactions in the DNA duplexes (we assume that the DNA duplexes undergo two-state transition), and the heat capacity [math]\displaystyle{ C_p }[/math] is constant over different temperatures. To reduce such inaccuracy in calculation, short DNA oligomers (less than 30 base pairs) were used to minimize the secondary interaction within the DNA molecule.
Sodium dependence of [math]\displaystyle{ \Delta S^o }[/math] and [math]\displaystyle{ \Delta G^o }[/math]
The entropy and free energy calculated from formula (1) above apply at 37oC and 1M NaCl. To extend the results to various salt condition, the following correction formulae have been derived by (***)
- [math]\displaystyle{ \Delta S^o [Na^+] = \Delta S^o [1M NaCl] + 0.368 \times N/2 \times ln[Na^+] }[/math]
- [math]\displaystyle{ \Delta G^o [Na^+] = \Delta G^o [1M NaCl] + 0.114 \times N/2 \times ln[Na^+] }[/math]
where N is the total number of phosphate in the duplex and [Na^+] is the total concentration of monovalent cations ([math]\displaystyle{ Na^+ }[/math], [math]\displaystyle{ K^+ }[/math], [math]\displaystyle{ NH^{4+} }[/math]) in the solution. [math]\displaystyle{ \Delta H^o }[/math] is assumed to be sodium-independent.
To calculate the value of [math]\displaystyle{ \Delta G^o }[/math] at temperature different than 37[math]\displaystyle{ ^o }[/math]C , the following equation is used:
[math]\displaystyle{ \Delta G^o = \Delta H^o - T\Delta S^o }[/math]
in which T is in Kelvin, [math]\displaystyle{ \Delta H^o }[/math] is in cal/mol, and [math]\displaystyle{ \Delta S^o }[/math] is in entropy units (e.u.). [math]\displaystyle{ \Delta H^o }[/math] and [math]\displaystyle{ \Delta S^o }[/math] are assumed to be independent of temperature.
The User Interface (GUI)
GUI or graphic user interface is constructed to create a friendly environment for users to construct their DNA origami. Our GUI is generated using Window form application in Visual studio 2010. Our software has three main components to support the DNA Origami design with sticky end addition and the themaldynamic analysis of sticky ends. The code sources are provided in the attachments.
Generate DNAO
For the first component, staples’ sequences used for the correct folding of DNA Origami with sticky ends are generated. User are required to define the size and shape of the structures they want to design by first input the frame size, and then choose the null squares (the location which will not be occupied by the scaffold). This would help the program to understand the DNA Origami design.
After obtaining the parameters required, the program will generate different possible scaffold ways and ask users to choose one of their interest.
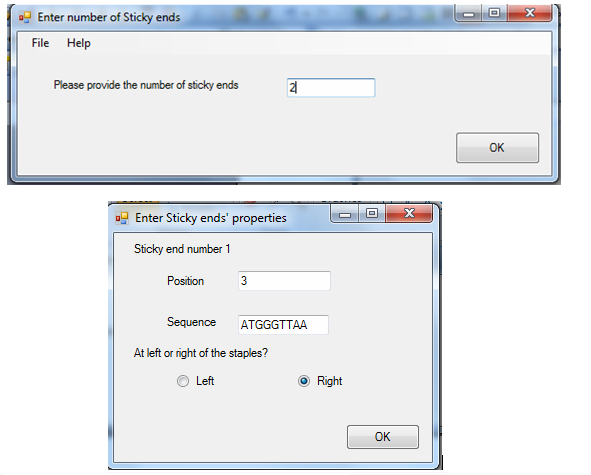
Users can also choose to add sticky end by enter the number of sticky end they need and specify the sequence and location of sticky ends in the scaffold.
Final staple sequences are generated and appear in the result window.
Generate sticky end sequence
To support generation of sticky end, as well as, to ensure that the sticky end will not affect the scaffold folding, an additional component is provided. User can choose to manually input a DNA sequence, and the program can help to check for the most stabilizing binding position in the scaffold. The binding energy is also calculated for users’ reference.
User can also ask the program to generate the sticky end sequence with the defined length. DNA sequences with binding energy higher than a limit defined are given. The below image illustrates the output of sticky ends' sequence generation.
Thermaldynamic analysis
The other component of the software is also to support the sticky end analysis in which thermal dynamic values of the sequence are calculated. Users need to enter the sequence they want to analyze, together with the condition in which they would test the DNA (total DNA strand concentration, Na+ concentration, and melting temperatures). Thermaldynamics value including deltaG, deltaS, deltaH, and Tm are provided in the results pages.