Mass Univariate ERP Toolbox: between-subject t-tests
Home/Download Tutorial Revision History Contact/Questions Appendix Other EEG Analysis Software Packages
Tutorial Sections
- Installing the Mass Univariate Toolbox
- Creating GND variables from EEGLAB set or ERPLAB erp files
- Within-subject t-tests
- Between-subject t-tests<-You are here
- General advice
The between-subjects analysis section of the tutorial uses the GND variables in the following two files for illustration:
Tones_female.GND
Tones_male.GND
They contain the ERPs to tones in a simple tone counting task in female and male participants respectively. To learn what a GND variable is and how to create your own GND variables, read the previous section of the tutorial on " Adding bin information to set files and creating GND variables."
Between-Subject t-Tests
Creating a GRP variable from two GND variables
The first step to detecting differences between two groups of participants is to construct a GRP variable, which collects the ERPs from both groups. This is done via the function GNDs2GRP.m. For example, let's analyze the difference between the ERPs to tones from women and men in the demo GND variables for this section of the tutorial. First download the GND variable containing the ERPs from women (Tones_female.GND) and men (Tones_male.GND). We can create a GRP variable (note "GRP" stands for "groups") from these files with the following command:
>> GRP=GNDs2GRP('gui','create_difs','yes');
A GUI should appear asking you which files containing GND variables you would like to include in the GRP variable.
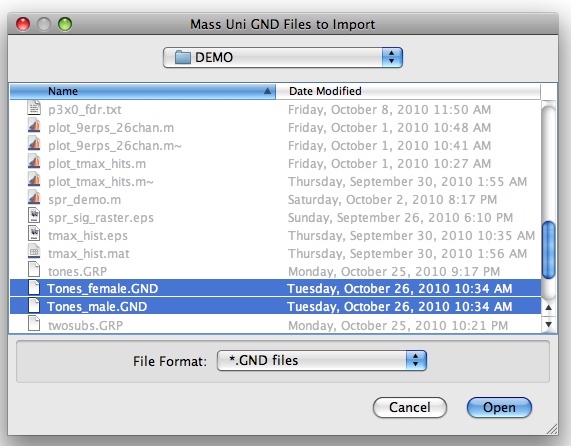
Select Tones_female.GND and Tones_male.GND and click open. You will then be asked if you want to add any more GND variables:
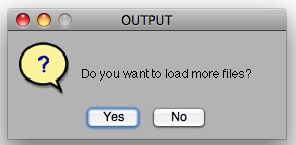
Click "no" and then you will be asked to name the group of participants from each GND file:

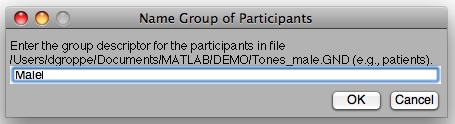
Call the first group "Female." Likewise, call the second group "Male":
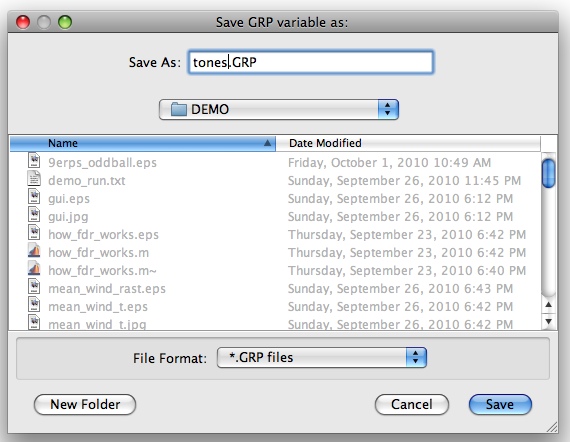
Finally, you'll be asked to provide a filename for the new GRP variable you've created. Use "tones.GRP":
You should now have GRP variable in your MATLAB workspace. You can see exactly what's in the GRP variable by typing "GRP into the command line:
>> GRP
GRP =
exp_desc: 'Tone Counting'
filename: 'tones.GRP'
filepath: '/Users/dgroppe/Documents/MATLAB/DEMO/'
saved: 'yes'
group_desc: {'Female' 'Male'}
GND_fnames: {'/Users/dgroppe/Documents/MATLAB/DEMO/Tones_female.GND' '/Users/dgroppe/Documents/MATLAB/DEMO/Tones_male.GND'}
grands: [31x127 double]
grands_stder: [31x127 double]
grands_t: [31x127 double]
chanlocs: [1x31 struct]
bin_info: [1x1 struct]
condesc: {'Experiment (not cal pulses)'}
time_pts: [1x127 double]
bsln_wind: [-96 -8]
odelay: 8
srate: 125
indiv_fnames: {{1x20 cell} {1x17 cell}}
indiv_subnames: {{1x20 cell} {1x17 cell}}
indiv_traits: {[] []}
indiv_bin_ct: {[20x1 double] [17x1 double]}
indiv_bin_raw_ct: {[20x1 double] [17x1 double]}
indiv_art_ics: {{1x20 cell} {1x17 cell}}
cals: [1x1 struct]
history: []
t_tests: []
Here's what the various fields store:
- exp_desc:<-the name of the experiment (this is taken from the source GND variables)
- filename:<-the filename of the GRP variable
- filepath: <-the filepath of the GRP variable
- saved: <-whether or not the GRP variable has been saved since it was last modified
- group_desc: <-strings indicating the name of each group in the GRP variable
- GND_fnames:<-the filenames and paths of the source GND variables used to make the GRP variable. Note, the source GND variables are accessed when new bins are added to the GRP variable. Thus if you move the location of the GND variables after creating the GRP variable, you will not be able to create new bins in the GRP variable (unless you update GRP.GND_fnames with the new file locations).
- grands: <-grand average ERPs (channel x time point x bin) in microvolts
- grands_stder: <-standard error of the grand average ERPs (channel x time point x bin) in microvolts
- grands_t: <-t-scores of the grand average ERPs (channel x time point x bin), which is simply the grand average divided by the standard error
- chanlocs: <-electrode coordinates in EEGLAB format
- bin_info: <-struct array containing the text definition of each bin, the number of participants from each group contributing to each bin, how the bin was produced from the two groups, and it's "condition code." Condition codes are specific to Kutaslab data and can be ignored by non-Kutaslab users. GRP.bin_info(#).op indicates if the bin contains a difference wave ('A-B') or the mean of the ERPs from the two groups ('A+B'). The rest of the fields indicate which group corresponds to Group A and Group B and which bins from each group were used.
- condesc: <-text descriptions of each condition code. Again, condition codes are specific to Kutaslab data and can be ignored by non-Kutaslab users.
- time_pts: <-the peri-event time that each ERP time point corresponds to (in milliseconds)
- bsln_wind: <-the time window used to baseline the ERPs (in milliseconds)
- odelay: <-A field specific to Kutaslab data that can be ignored by non-Kutaslab users
- srate: <-Data sampling rate (in Hz)
- indiv_fnames: <-The filenames of the set files used to produce the source GND variables
- indiv_subnames: <-The codenames of each subject in each of the two groups
- indiv_traits: <-A field where you could store traits of individual subjects (e.g., age, working memory span)
- indiv_bin_ct: <-The number of trials each participant contributed to each bin
- indiv_bin_raw_ct: <-A field specific to Kutaslab data that can be ignored by non-Kutaslab users.
- indiv_art_ics: <-The numeric indices of independent components removed from each set file before using them to compute ERPs
- cals: <-A field specific to Kutaslab data that can be ignored by non-Kutaslab users
- history: <-A record of commands applied to the GRP variable
- t_tests: <-The results of mass univariate t-test analyses applied to this GRP variable
A more readable way to know the basic contents of a GND variable is to use the function headinfo.m ("headinfo" is short for header information):
>> headinfo(GRP)
CHANNELS
1:lle 2:lhz 3:MiPf 4:LLPf 5:RLPf 6:LMPf 7:RMPf 8:LDFr
9:RDFr 10:LLFr 11:RLFr 12:LMFr 13:RMFr 14:LMCe 15:RMCe 16:MiCe
17:MiPa 18:LDCe 19:RDCe 20:LDPa 21:RDPa 22:LMOc 23:RMOc 24:LLTe
25:RLTe 26:LLOc 27:RLOc 28:MiOc 29:A2 30:rhz 31:rle
GROUPS
Group 1: Female (20 participants)
Group 2: Male (17 participants)
BINS
Bin 1: Tones (Counting) (Female-Male)
t-TESTS
No t-test results have been stored with these data.
Note that the GRP variable has one bin. This is because we used the 'create_difs' option when we created the GRP variable with GNDs2GRP.m, which automatically creates a difference wave between all bins in the two GND variables. The function bin_opGRP.m can also be used to add bins to a GRP variable. For example, we can add a bin that is the mean of the ERPs to tones in men and women like so:
>>GRP=bin_opGRP(GRP,'(A+B)/n','Female',1,'Male',1,'Tone Counting Task (mean of Female and Male)');
To see the ERPs in the GRP variable, use the ERP GUI:
>> gui_erp(GRP)

By looking at Bin 1, you can see the difference between men and women has two peaks: a negativity that peaks around 72 ms and positivity that peaks around 128 ms. By looking at Bin 2, the mean ERPs to tones from men and women, you can see a clear P1-N1-P2 series of auditory components.
Time point by time point analysis
tmax permutation test
To see if the early auditory ERP components differ between men and women, we can perform a tmax permutation test based on the independent samples t-statistic at every time point from 25 to 250 ms and every scalp electrode. Note, that this GRP variable contains data at ocular electrodes and the right mastoid. Since we don't anticipate any differences at those electrodes, we can remove them from the analysis to increase the power of the test at the remaining electrodes. The following command executes the test:
>>GRP=tmaxGRP(GRP,1,'time_wind',[25 250],'exclude_chans',{'lhz','rhz','lle','rle','A2'});
This should produce the following output on the MATLAB command line:
Experiment: Tone Counting
Time Window #1:
Attempting to use time boundaries of 25 to 250 ms for hypothesis test.
Exact window boundaries are 24 to 248 ms (that's from time point 16 to 44).
Loading individual participant ERPs from Bin 1 (Tones (Counting)) of GND variable from /Users/dgroppe/Documents/MATLAB/DEMO/Tones_female.GND.
Loading individual participant ERPs from Bin 1 (Tones (Counting)) of GND variable from /Users/dgroppe/Documents/MATLAB/DEMO/Tones_male.GND.
Testing null hypothesis that the grand average ERPs in GRP variable's Bin 1 (Tones (Counting) (Female-Male)) have a mean of 0.000000 microvolts.
Alternative hypothesis is that the ERPs differ from 0.000000 (i.e., two-tailed test).
Performing independent samples t-tests.
mxt_perm2: Number of channels: 26
mxt_perm2: Number of time points: 29
mxt_perm2: Total # of comparisons: 754
mxt_perm2: Number of participants in Group A: 20
mxt_perm2: Number of participants in Group B: 17
t-score degrees of freedom: 35
Executing permutation test with 2500 permutations...
Permutations completed: 100, 200, 300, 400, 500, 600, 700, 800, 900, 1000
1100, 1200, 1300, 1400, 1500, 1600, 1700, 1800, 1900, 2000
2100, 2200, 2300, 2400, 2500
Desired family-wise alpha level: 0.050000
Estimated actual family-wise alpha level: 0.050000
Critical t-score(s):-3.978 3.978
That corresponds to a test-wise alpha level of 0.000333.
Bonferroni test-wise alpha would be 0.000066.
ERPs are NOT significantly different from zero (alpha=0.050000) at any time point/window analyzed.
All p-values>=0.181200
Save GRP variable as /Users/dgroppe/Documents/MATLAB/DEMO/tones.GRP? (y or n) y
GRP variable successfully saved to disk.
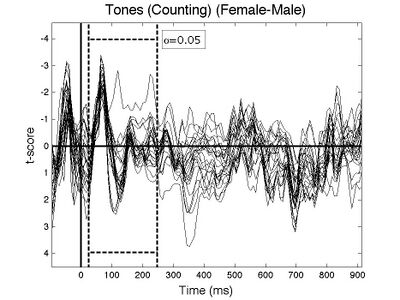
And the ERP GUI and a "sig_raster" plot should be produced illustrating the outcome of the test:

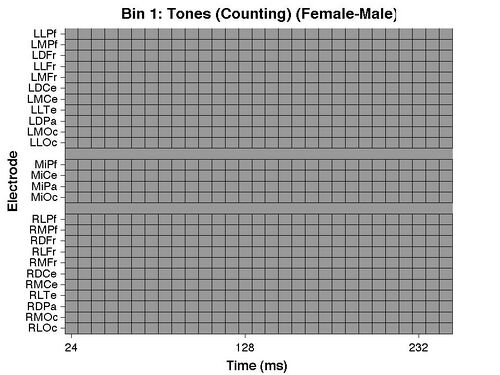
For more information on these plots see the section of the tutorial on Within-subject t-tests. As you can see from both plots, and the command line output, the analysis found no significant differences between men and women.
To reproduce these figures without redoing the permutation test, enter the following:
>> sig_raster(GRP,1);
>> gui_erp(GRP,'t_test',1);
You can also make a black and white butterfly plot of the analysis for publication with the sig_wave.m function:
>>sig_wave(GRP,1,'use_color','no','wave_limits',[-4.6 4.5],'fig_id',10);
This example showed you the very basics of using tmaxGRP. The function has many optional arguments that may be of interest (e.g., doing one-tailed tests, performing tests in multiple non-contiguous time windows). To see the full list of options for tmaxGRP enter:
>> help tmaxGRP
t-tests with control of the false discovery rate
Instead of using the tmax permutation procedure to deal with the large number of comparisons, you can use one of various methods from Benjamini and colleagues to control the false discovery rate (i.e., the mean proportion of significant tests that are false discoveries). You can do this with the function tfdrGRP.m, which functions very similarly to tmaxGRP. To repeat the analysis performed with the tmax procedure above using the Benjamini and Yekutieli algorithm for control of the false discovery rate, enter the following:
>> GRP=tfdrGRP(GRP,1,'method','by','time_wind',[25 250],'exclude_chans',{'lhz','rhz','lle','rle','A2'});
As with tmaxGRP, tfdrGRP has many optional arguments that may be of interest (e.g., doing one-tailed tests, performing tests in multiple non-contiguous time windows). To see the full list of options for tfdrGRP enter:
>> help tfdrGRP
cluster mass permutation test
A third alternative for correcting for a large number of comparisons is to use a cluster-based permutation test (Bullmore et al., 1999). You can do this using the cluster mass statistic with the function clustGRP.m, which functions very similarly to tmaxGRP.m. To repeat the analysis performed with the tmax procedure using a cluster-based test, enter the following:
>> GRP=clustGRP(GRP,1,'time_wind',[25 250],'exclude_chans',{'lhz','rhz','lle','rle','A2'},'chan_hood',.61,'thresh_p',.05);
As with tmaxGRP, clustGRP has many optional arguments that may be of interest (e.g., doing one-tailed tests, performing tests in multiple non-contiguous time windows). To see the full list of options for clustGRP enter:
>> help clustGRP
Mean time window analysis
tmax permutation test
Instead of performing t-tests at every single time point, it is also possible to perform t-test on mean ERP or difference wave amplitude in a particular time window. For example, say we had reason to believe that the ERPs to tones between men and women should differ in two time windows: 60-90 and 90-150 ms. We can perform t-tests in those two windows at every electrode using the tmax permutation procedure as follows:
>> GRP=tmaxGRP(GRP,1,'time_wind',[60 90; 95 150],'mean_wind','yes');
This should produce the following command line output:
Experiment: Tone Counting
Time Window #1:
Attempting to use time boundaries of 60 to 90 ms for hypothesis test.
Exact window boundaries are 56 to 88 ms (that's from time point 20 to 24).
Time Window #2:
Attempting to use time boundaries of 95 to 150 ms for hypothesis test.
Exact window boundaries are 96 to 152 ms (that's from time point 25 to 32).
Loading individual participant ERPs from Bin 1 (Tones (Counting)) of GND variable from /Users/dgroppe/Documents/MATLAB/DEMO/Tones_female.GND.
Loading individual participant ERPs from Bin 1 (Tones (Counting)) of GND variable from /Users/dgroppe/Documents/MATLAB/DEMO/Tones_male.GND.
Testing null hypothesis that the grand average ERPs in GRP variable's Bin 1 (Tones (Counting) (Female-Male)) have a mean of 0.000000 microvolts.
Alternative hypothesis is that the ERPs differ from 0.000000 (i.e., two-tailed test).
Performing independent samples t-tests.
mxt_perm2: Number of channels: 31
mxt_perm2: Number of time points: 2
mxt_perm2: Total # of comparisons: 62
mxt_perm2: Number of participants in Group A: 20
mxt_perm2: Number of participants in Group B: 17
t-score degrees of freedom: 35
Executing permutation test with 2500 permutations...
Permutations completed: 100, 200, 300, 400, 500, 600, 700, 800, 900, 1000
1100, 1200, 1300, 1400, 1500, 1600, 1700, 1800, 1900, 2000
2100, 2200, 2300, 2400, 2500
Desired family-wise alpha level: 0.050000
Estimated actual family-wise alpha level: 0.050000
Critical t-score(s):-3.2863 3.2863
That corresponds to a test-wise alpha level of 0.002314.
Bonferroni test-wise alpha would be 0.000806.
ERPs are NOT significantly different from zero (alpha=0.050000) at any time point/window analyzed.
All p-values>=0.225600
Save GRP variable as /Users/dgroppe/Documents/MATLAB/DEMO/tones.GRP? (y or n) y
GRP variable successfully saved to disk.
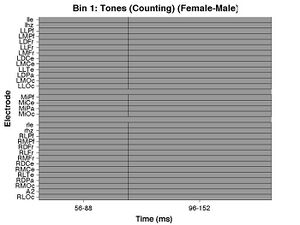
The following figures should be produced as well. The first is a raster diagram. White squares would indicate electrodes/time windows in which the ERPs to targets are significantly more positive, but there are no significant differences between women and men in this analysis either.
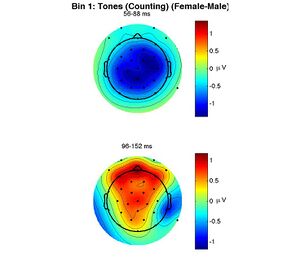
The other two figures produced are the topographies of the mean amplitude of the female-male difference wave in the two time windows analyzed. In one figure the topographies are in units of microvolts, in the other, they are shown as t-scores. White circles would indicate electrodes for which the ERPs to targets and standards are significantly different.
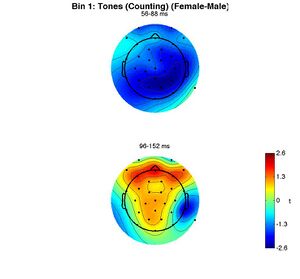
To reproduce these figures without redoing the permutation test, enter the following:
>> sig_raster(GRP,3);
>> sig_topo(GRP,4,'units','uV');
>> sig_topo(GRP,4,'units','t');
t-tests with control of the false discovery rate
Again, instead of using the tmax permutation procedure to deal with the large number of comparisons, you can use one of various methods from Benjamini and colleagues to control the false discovery rate using the function tfdrGRP.m. To repeat the mean time window analysis performed with the tmax procedure above using the Benjamini and Yekutieli algorithm for control of the false discovery rate, enter the following:
>> GRP=tfdrGRP(GRP,1,'time_wind',[60 90; 95 150],'mean_wind','yes','method','by');
cluster mass permutation test
Instead of using the tmax permutation procedure or FDR control to deal with the large number of comparisons, you can use a cluster-based permutation test via the function clustGRP.m. To perform a between-subjects analysis on the mean ERP amplitude in the N1 time window using a permutation test based on the cluster mass statistic, enter the following:
>> GRP=clustGRP(GRP,1,'time_wind',[95 150],'mean_wind','yes','chan_hood',.61,'thresh_p',.05);
Note, unlike tmaxGRP and tfdrGRP, clustGRP currently only supports tests on a single time window.
Sample methods description
To help you write up your own applications of these methods, below are example methods section descriptions of some of the analyses performed above:
tmax permutation test
For the time point by time point analysis performed here:
LONG VERSION:
To detect reliable differences between the ERPs to tones from women and men in the tone counting task, these ERPs were submitted to an independent samples, two-tailed permutation test based on the tmax statistic (Blair & Karniski, 1993) using a family-wise alpha level of 0.05. All time points between 25 and 250 ms at all 26 scalp electrodes were included in the test (i.e., 754 total comparisons). Independent samples t-tests (assuming equal variance in the two groups) were performed for each comparison using the original data and 2500 random between-participant permutations of the data (i.e., for each permutation participants were randomly assigned to one of the two groups without replacement). The t-scores from each comparison were converted to their absolute values* and the greatest t-score in each of the 2500 sets of tests (i.e., the "tmax" of each set of tests) was recorded and used to estimate the tmax distribution of the null hypothesis (i.e., no difference between conditions**). Based on this estimate, critical t-scores of +/- 3.98 (df=35) were derived. In other words, any differences in the original data that exceeded a t-score of +/-3.98 were deemed reliable.
This permutation test analysis was used in lieu of more conventional mean amplitude ANOVAs because it provides much better spatial and temporal resolution than conventional ANOVAs while maintaining a desired family-wise alpha level (i.e., it effectively corrects for the large number of comparisons). Moreover, the tmax statistic was chosen for this permutation test because it has been shown to have relatively good power for data (like ERPs) whose dimensions are highly correlated (Hemmelman et al., 2004). 2500 permutations were used to estimate the distribution of the null hypothesis as it is more than twice the number recommend by Manly (1997) for a family-wise alpha level of 0.05. No reliable differences were found (all p>0.18).
*Footnote: The t-scores were converted to absolute values to make the test a two-tailed test.
**Footnote: More specifically, the null hypothesis of the permutation test is that participants in the two groups are "exchangeable" (i.e., the ERPs from a female participant could have just as likely come from a male participant and vice-versa).
SHORT VERSION:
To detect reliable differences between the ERPs to tones from women and men in the tone counting task, these ERPs were submitted to an independent samples, two-tailed permutation test based on the tmax statistic (Blair & Karniski, 1993) using a family-wise alpha level of 0.05. All time points between 25 and 250 ms at all 26 scalp electrodes were included in the test (i.e., 754 total comparisons). 2500 random within-participant permutations of the data were used to estimate the distribution of the null hypothesis (i.e., no difference between conditions). Based on this estimate, critical t-scores of +/- 3.98 (df=35) were derived. In other words, any differences in the original data that exceeded a t-score of +/-3.98 were deemed reliable. No reliable differences were found (all p>0.18).
- Blair, R. C., & Karniski, W. (1993). An alternative method for significance testing of waveform difference potentials. Psychophysiology, 30(5), 518-524.
- Hemmelmann, C., Horn, M., Reiterer, S., Schack, B., Susse, T., & Weiss, S. (2004). Multivariate tests for the evaluation of high-dimensional EEG data. Journal of Neuroscience Methods, 139(1), 111-120
- Manly, B. F. J. (1997). Randomization, bootstrap, and Monte Carlo methods in Biology (2nd ed.). London: Chapman & Hall.
t-tests with control of the false discovery rate
For the time point by time point analysis performed here:
LONG VERSION:
To detect reliable differences between the ERPs to men and women in the tone counting task, the ERPs from these conditions were submitted to independent samples two-tailed t-tests at all time points between 25 and 250 ms at all 26 scalp electrodes (i.e., 754 total comparisons). The Benjamini & Yekutieli (2001) procedure for control of the false discovery rate* (FDR) was applied to assess the significance of each test using an FDR level of 5%. This particular FDR procedure guarantees that the true FDR will be less than or equal to the nominal FDR level of 5% regardless of the dependency structure of the multiple tests.
This massive univariate analysis was used in lieu of more conventional mean amplitude ANOVAs because it provides much better spatial and temporal resolution than conventional ANOVAs while maintaining reasonable limits on the likelihood of false discoveries (i.e., it provides a reasonable correction for the large number of comparisons).
*Footnote: The false discovery rate is the mean proportion of significant test results that are actually false discoveries (i.e., Type I errors). The analysis found no significant differences between men and women.
SHORT VERSION:
To detect reliable differences between the ERPs to men and women in the tone counting task, the ERPs from these conditions were submitted to independent samples two-tailed t-tests at all time points between 25 and 250 ms at all 26 scalp electrodes (i.e., 754 total comparisons). The Benjamini & Yekutieli (2001) procedure for control of the false discovery rate* (FDR) was applied to assess the significance of each test using an FDR level of 5%. This particular FDR procedure guarantees that the true FDR will be less than or equal to the nominal FDR level of 5% regardless of the dependency structure of the multiple tests. The analysis found no significant differences between men and women.
- Benjamini, Y., & Yekutieli, D. (2001). The control of the false discovery rate in multiple testing under dependency. The Annals of Statistics, 29(4), 1165-1188.
cluster-based permutation test
For the time point by time point analysis performed here:
LONG VERSION:
To detect reliable differences between the ERPs to tones from women and men in the tone counting task, these ERPs were submitted to an independent samples, two-tailed permutation test based on the cluster mass statistic (Bullmore et al., 1999) using a family-wise alpha level of 0.05. All time points between 25 and 250 ms at all 26 scalp electrodes were included in the test (i.e., 754 total comparisons). Independent samples t-tests (assuming equal variance in the two groups) were performed for each comparison using the original data and 2500 random between-participant permutations of the data (i.e., for each permutation participants were randomly assigned to one of the two groups without replacement). t-scores corresponding to an uncorrected p-value of 0.05 or less were formed into clusters with any neighboring such t-scores. Electrodes within approximately 5.44 cm of one another were considered spatial neighbors and adjacent time points were considered temporal neighbors. The sum of the t-scores in each cluster is the "mass" of that cluster and the most extreme cluster mass in each of the 2501 sets of tests was recorded and used to estimate the distribution of the null hypothesis (i.e., no difference between conditions*). The permutation cluster mass percentile ranking of each cluster from the observed data was used to derive its p-value. The p-value of the cluster was assigned to each member of the cluster and t-scores that were not included in a cluster were given a p-value of 1.
This permutation test analysis was used in lieu of more conventional mean amplitude ANOVAs because it provides much better spatial and temporal resolution than conventional ANOVAs while maintaining weak control of the family-wise alpha level (i.e., it corrects for the large number of comparisons). Moreover, the cluster mass statistic was chosen for this permutation test because it has been shown to have relatively good power for broadly distributed ERP effects like the P300 (Groppe et al., 2011; Maris & Oostenveld, 2007). 2500 permutations were used to estimate the distribution of the null hypothesis as it is over twice the number recommend by Manly (1997) for a family-wise alpha level of 0.05. No reliable differences were found (all p>0.17).
*Footnote: More specifically, the null hypothesis of the permutation test is that participants in the two groups are "exchangeable" (i.e., the ERPs from a female participant could have just as likely come from a male participant and vice-versa).
SHORT VERSION:
To detect reliable differences between the ERPs to tones from women and men in the tone counting task, these ERPs were submitted to an independent samples, two-tailed permutation test based on the cluster mass statistic (Bullmore et al., 1999) using a family-wise alpha level of 0.05. All time points between 25 and 250 ms at all 26 scalp electrodes were included in the test (i.e., 754 total comparisons). Independent samples t-tests (assuming equal variance in the two groups) were performed for each comparison using the original data and 2500 random between-participant permutations of the data. t-scores corresponding to an uncorrected p-value of 0.05 or less were formed into clusters with any neighboring such t-scores. Electrodes within approximately 5.44 cm of one another were considered spatial neighbors and adjacent time points were considered temporal neighbors. No reliable differences were found (all p>0.17).
- Bullmore, E. T., Suckling, J., Overmeyer, S., Rabe-Hesketh, S., Taylor, E., & Brammer, M. J. (1999). Global, voxel, and cluster tests, by theory and permutation, for a difference between two groups of structural MR images of the brain. IEEE Transactions on Medical Imaging, 18(1), 32-42
- Groppe, D. M., Urbach, T. P., & Kutas, M. (2011). Mass univariate analysis of event-related brain potentials/fields II: Simulation studies. Psychophysiology.
- Manly, B. F. J. (1997). Randomization, Bootstrap, and Monte Carlo Methods in Biology (2nd ed.). London: Chapman & Hall.
- Maris, E., & Oostenveld, R. (2007). Nonparametric statistical testing of EEG- and MEG-data. Journal of Neuroscience Methods, 164(1), 177-190.
Summary of relevant functions
- bin_opGRP: A function that creates a new bin in a GRP variable that is the difference between or mean of two existing bins.
- fast_t2: The function called by tfdrGRP.m that computes independent samples t-tests.
- GNDs2GRP: Creates a GRP struct variable from two GND variables.
- gui_erp: Creates a GUI for exploring the ERPs in a GRP (or GND) variable. Visualizes ERP standard error of the mean, t-scores, and global field power as well. Useful for visualizing the results of mass univariate t-tests and exploring your data.
- headinfo: Summarizes the contents of a GRP (or GND) variable.
- mxt_perm2: The function called by tmaxGRP.m that actually computes a one-sample/repeated measures tmax permutation test.
- rm_bins: Removes one or more bins (and associated permutation test results) from a GRP (or GND) variable.
- rm_ttest: Removes one or more permutation/FDR t-test test results from a GRP (or GND) variable.
- save_erps: Saves a GRP (or GND) struct variable to disk.
- sig_raster: Creates a two-dimensional binary "raster" diagram (Channel x Time) for visualizing the results of mass univariate tests.
- sig_topo: Plots ERP/ERP-effect topographies for t-tests performed on ERPs/difference waves after averaging voltage within one or more time windows.
- tfdrGRP: Performs independent samples t-tests on multiple electrodes and multiple time points. Significance thresholds are determined by using a procedure to control the false discovery rate. The function currently supports three procedures for FDR control: the original Benjamini & Hochberg algorithm (1995) and two variants of that method.
- tmaxGRP: Effectively performs independent samples t-tests on multiple electrodes and multiple time points via a tmax permutation test. This procedure controls the family-wise error rate at a specified level (like Bonferroni correction).
